|
|
|
|
|
| XC3000 | XC4000E | XC4000X | XC5200 | XC9000 | Spartan | SpartanXL | Spartan2 | Virtex |
|---|---|---|---|---|---|---|---|---|
| Macro | Macro | Macro | Macro | Macro | Macro | Macro | Macro | Macro |
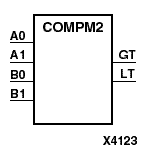
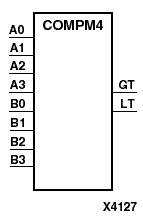
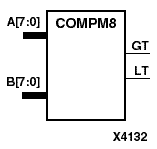
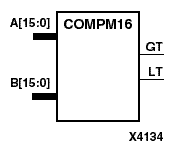
COMPM2, COMPM4, COMPM8, and COMPM16 are, respectively, 2-, 4-, 8-, and 16-bit magnitude comparators that compare two positive binary-weighted words.
COMPM2 compares A1 - A0 and B1 - B0, where A1 and B1 are the most significant bits. COMPM4 compares A3 - A0 and B3 - B0, where A3 and B3 are the most significant bits. COMPM8 compares A7 - A0 and B7 - B0, where A7 and B7 are the most significant bits. COMPM16 compares A15 - A0 and B15 - B0, where A15 and B15 are the most significant bits.
The greater-than output (GT) is High when A>B, and the less-than output (LT) is High when A<B. When the two words are equal, both GT and LT are Low. Equality can be measured with this macro by comparing both outputs with a NOR gate.
| Inputs | Outputs | ||||
|---|---|---|---|---|---|
| A1 | B1 | A0 | B0 | GT | LT |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | X | X | 1 | 0 |
| 0 | 1 | X | X | 0 | 1 |
| Inputs | Outputs | ||||
|---|---|---|---|---|---|
| A3, B3 | A2, B2 | A1, B1 | A0, B0 | GT | LT |
| A3>B3 | X | X | X | 1 | 0 |
| A3<B3 | X | X | X | 0 | 1 |
| A3=B3 | A2>B2 | X | X | 1 | 0 |
| A3=B3 | A2<B2 | X | X | 0 | 1 |
| A3=B3 | A2=B2 | A1>B1 | X | 1 | 0 |
| A3=B3 | A2=B2 | A1<B1 | X | 0 | 1 |
| A3=B3 | A2=A2 | A1=B1 | A0>B0 | 1 | 0 |
| A3=B3 | A2=B2 | A1=B1 | A0<B0 | 0 | 1 |
| A3=B3 | A2=B2 | A1=B1 | A0=B0 | 0 | 0 |
| Inputs | Outputs | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| A7, B7 | A6, B6 | A5, B5 | A4, B4 | A3, B3 | A2, B2 | A1, B1 | A0, B0 | GT | LT |
| A7>B7 | X | X | X | X | X | X | X | 1 | 0 |
| A7<B7 | X | X | X | X | X | X | X | 0 | 1 |
| A7=B7 | A6>B6 | X | X | X | X | X | X | 1 | 0 |
| A7=B7 | A6<B6 | X | X | X | X | X | X | 0 | 1 |
| A7=B7 | A6=B6 | A5>B5 | X | X | X | X | X | 1 | 0 |
| A7=B7 | A6=B6 | A5<B5 | X | X | X | X | X | 0 | 1 |
| A7=B7 | A6=B6 | A5=B5 | A4>B4 | X | X | X | X | 1 | 0 |
| A7=B7 | A6=B6 | A5=B5 | A4<B4 | X | X | X | X | 0 | 1 |
| A7=B7 | A6=B6 | A5=B5 | A4=B4 | A3>B3 | X | X | X | 1 | 0 |
| A7=B7 | A6=B6 | A5=B5 | A4=B4 | A3<B3 | X | X | X | 0 | 1 |
| A7=B7 | A6=B6 | A5=B5 | A4=B4 | A3=B3 | A2>B2 | X | X | 1 | 0 |
| A7=B7 | A6=B6 | A5=B5 | A4=B4 | A3=B3 | A2<B2 | X | X | 0 | 1 |
| A7=B7 | A6=B6 | A5=B5 | A4=B4 | A3=B3 | A2=B2 | A1>B1 | X | 1 | 0 |
| A7=B7 | A6=B6 | A5=B5 | A4=B4 | A3=B3 | A2=B2 | A1<B1 | X | 0 | 1 |
| A7=B7 | A6=B6 | A5=B5 | A4=B4 | A3=B3 | A2=B2 | A1=B1 | A0>B0 | 1 | 0 |
| A7=B7 | A6=B6 | A5=B5 | A4=B4 | A3=B3 | A2=B2 | A1=B1 | A0<B0 | 0 | 1 |
| A7=B7 | A6=B6 | A5=B5 | A4=B4 | A3=B3 | A2=B2 | A1=B1 | A0=B0 | 0 | 0 |
Figure 4.44 COMPM8 Implementation XC3000, XC4000E, XC4000X, XC5200, Spartan, SpartanXL, Spartan2, VirtexFigure 4.45 COMPM8 Implementation XC9000